Datengraph

Schauen wir uns Freundschaften einmal mathematisch an. Du kannst alle Graphen selbst mit deinen Graphen berechnen und auch interaktiv ausprobieren:

https://colab.research.google.com/drive/10D6_XI0jkiru30QGVNmu7nDGMmAvbFwm?usp=sharing

Gesamtnetzwerk (Degree)

Zeigt die allgemeine Vernetzung jedes Benutzers im gesamten Netzwerk.

Wertebereich: 0 bis 1

Berechnung: Anzahl der Verbindungen (ein- und ausgehend) eines Knotens, geteilt durch die maximal mögliche Anzahl von Verbindungen (n-1, wobei n die Gesamtzahl der Knoten ist)

Aufgabe

Welche Nutzer sind besonders stark vernetzt? Wer am wenigsten?

Prestige-Netzwerk (In-Degree)

Zeigt, wie "populär" oder "einflussreich" ein Benutzer ist, basierend auf der Anzahl der eingehenden Verbindungen.

Wertebereich: 0 bis 1

Berechnung: Anzahl der eingehenden Verbindungen eines Knotens, geteilt durch (n-1)

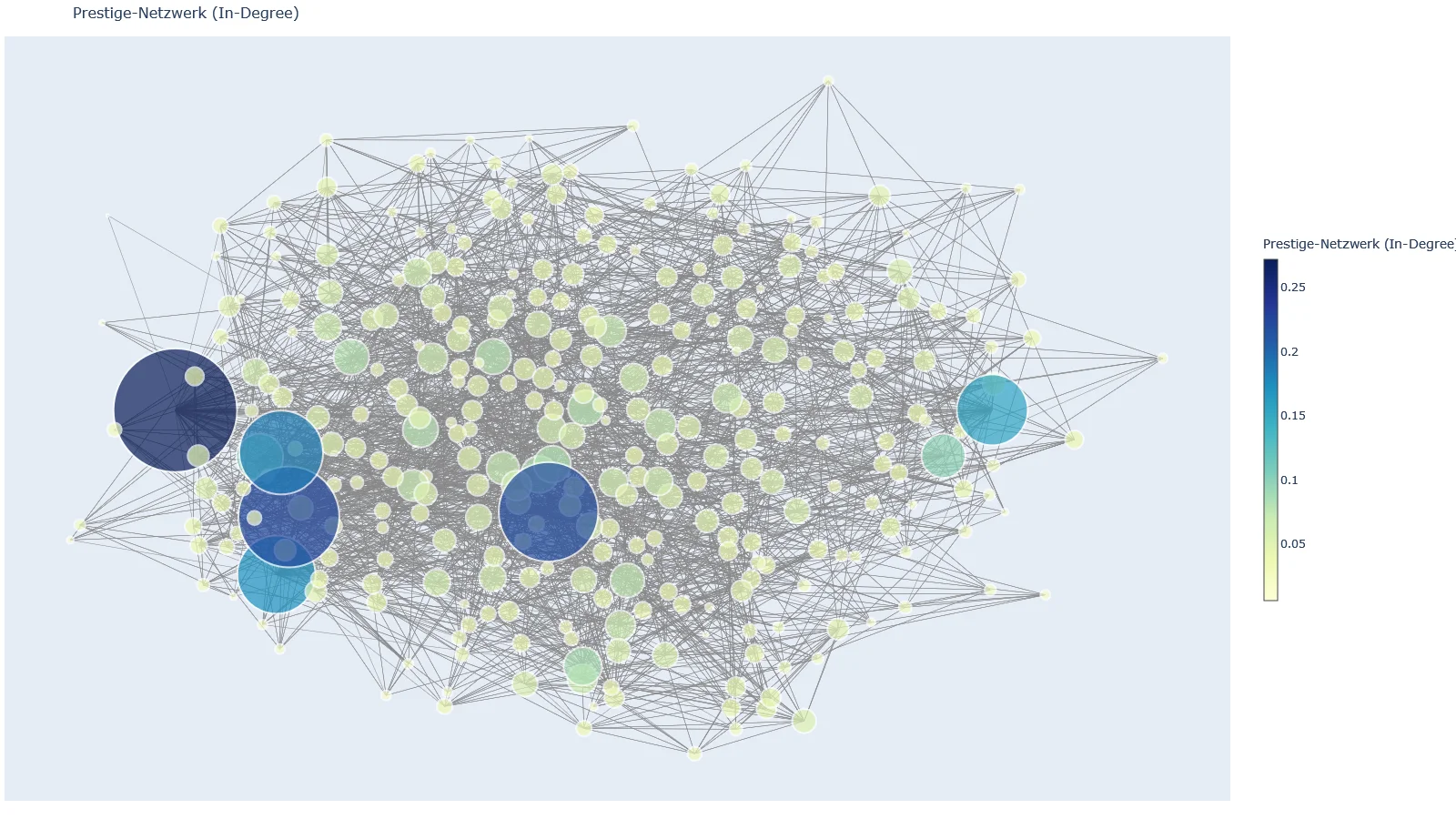
Aufgabe

Welche Nutzer sind besonders populär? Gibt es Schnittmengen zur Degree-Betrachtung?

Freundschaftsnetzwerk

Zeigt gegenseitige Verbindungen (Freundschaften) zwischen Benutzern.

Wertebereich: Ganzzahlige Werte, abhängig von der Anzahl der gegenseitigen Verbindungen

Berechnung: Knotengröße: ((v / max_size) ** 0.5) * 30, wobei v die Anzahl der Freundschaften und max_size die maximale Anzahl von Freundschaften im Netzwerk ist. ** 0.5 ist die Quadratwurzel. Wir verwenden sie, um die Unterschiede zwischen großen und kleinen Werten zu verringern. * 30 ist ein Skalierungsfaktor, den wir durch Experimentieren gefunden haben. Er macht die Knoten groß genug, um sichtbar zu sein, aber nicht so groß, dass sie sich zu sehr überlappen.

Aufgabe

Welche Nutzer haben besonders viele Freunde? Gibt es Schnittmengen zum Prestige der jeweiligen Nutzer?

Eigenvektor-Zentralität

Misst den Einfluss eines Knotens im Netzwerk, basierend auf der Wichtigkeit seiner Verbindungen. Die Wichtigkeit eines Knotens hängt nicht nur davon ab, wie viele Verbindungen er hat, sondern auch davon, wie wichtig diese Verbindungen sind. Stellt euch vor, ihr bewertet die Beliebtheit von Schüler:innen in einer Klasse. Ein:e Schüler:in gilt als besonders beliebt, wenn er oder sie nicht nur viele Freund:innen hat, sondern wenn diese Freund:innen selbst auch beliebt sind.

Wertebereich: Normalisiert auf 0 bis 1

Berechnung: Iterativer Algorithmus, der die Zentralität eines Knotens basierend auf den Zentralitäten seiner Nachbarn berechnet

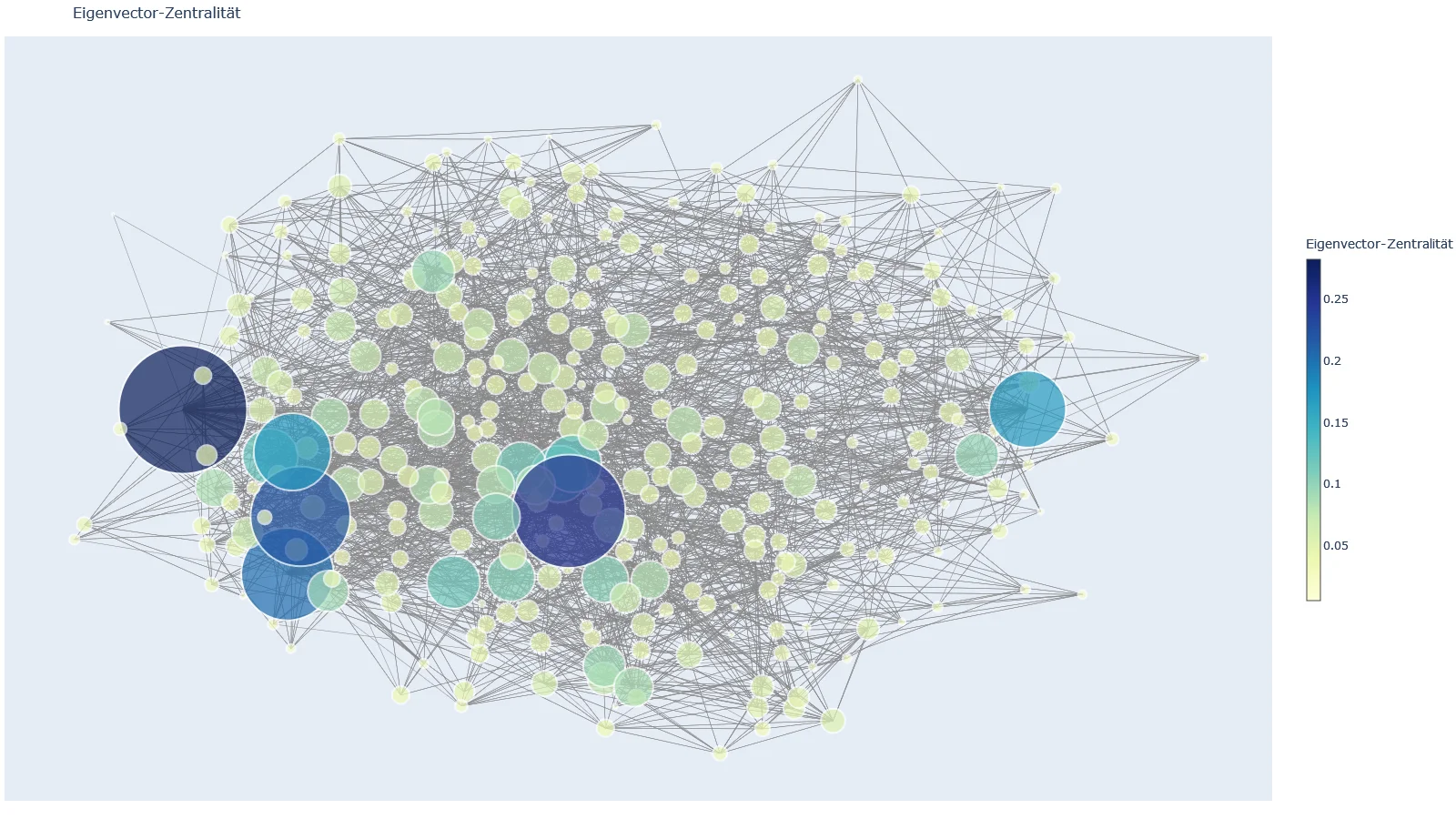
Aufgabe

Wer profitiert insbesondere von der Eigenvektorbetrachtung?

Eigenvector-Zentralität ausführlich erklärt

Hier ist eine präzisere Erklärung des Eigenvektor-Zentralitäts-Algorithmus:

1. Startzustand:
   • Jeder Knoten (Schüler:in) beginnt mit einem gleichen Wert, typischerweise 1.
2. In jeder Runde:
   • Jeder Knoten gibt seinen gesamten aktuellen Wert an jeden seiner Nachbarn weiter.
   • Ein Knoten mit Wert x und n Verbindungen gibt also x an jeden seiner n Nachbarn.
3. Neue Werte berechnen:
   • Der neue Wert eines Knotens ist die Summe aller Werte, die er von seinen Nachbarn erhalten hat.
4. Normalisierung:
   • Nach jeder Runde werden alle Werte normiert, indem man sie durch den größten Wert teilt.
   • Dies hält die Werte zwischen 0 und 1 und verhindert, dass sie ins Unendliche wachsen.
5. Wiederholung:
   • Dieser Prozess wird mehrmals wiederholt, bis sich die Werte kaum noch ändern.

Beispiel: Nehmen wir ein einfaches Netzwerk mit vier Schüler:innen: Anna, Ben, Clara und David. Anna ist mit Ben und Clara verbunden, Ben mit Anna und David, Clara mit Anna, und David mit Ben.

Runde 0 (Start): Alle haben den Wert 1.

Runde 1:

• Anna gibt 1 an Ben und 1 an Clara.
• Ben gibt 1 an Anna und 1 an David.
• Clara gibt 1 an Anna.
• David gibt 1 an Ben.

Neue Werte vor Normalisierung:

• Anna: 2 (von Ben und Clara)
• Ben: 2 (von Anna und David)
• Clara: 1 (von Anna)
• David: 1 (von Ben)

Nach Normalisierung (geteilt durch 2):

• Anna: 1
• Ben: 1
• Clara: 0.5
• David: 0.5

Runde 2:

• Anna gibt 1 an Ben und 1 an Clara.
• Ben gibt 1 an Anna und 1 an David.
• Clara gibt 0.5 an Anna.
• David gibt 0.5 an Ben.

Neue Werte vor Normalisierung:

• Anna: 1.5 (1 von Ben + 0.5 von Clara)
• Ben: 1.5 (1 von Anna + 0.5 von David)
• Clara: 1 (von Anna)
• David: 1 (von Ben)

Nach Normalisierung (geteilt durch 1.5):

• Anna: 1
• Ben: 1
• Clara: 0.67
• David: 0.67

Dieser Prozess wird fortgesetzt, bis sich die Werte stabilisieren. Die endgültigen normalisierten Werte sind dann die Eigenvektor-Zentralitätswerte der Knoten.

Diese Methode berücksichtigt nicht nur die Anzahl der Verbindungen, sondern auch deren "Qualität", da Verbindungen zu wichtigeren Knoten mehr zum eigenen Wert beitragen.

📝 Aufgaben

📝 Schulprojektgruppen

In deiner Klasse sollt ihr Projektgruppen bilden. Dein:e Lehrer:in hat Daten darüber, wie ihr miteinander vernetzt seid.

1. Handelt es sich bei Freundschaften in einer Schulklasse um einen gerichteten oder ungerichteten Graphen? Begründe deine Entscheidung.

2. Welches Netzwerkmaß würdest du nutzen, um...

   • herauszufinden, wer gut als Gruppenleiter:in geeignet ist?
   • zu erkennen, wer vielleicht Unterstützung braucht, um besser integriert zu werden?
   • zu finden, wer einen guten Überblick über die Klasse hat und gut darüber berichten könnte?

3. Hier sind die Werte für drei Mitschüler:innen:

Alex:
- Degree: 0.8
- Eigenvector: 0.4

Kim:
- Degree: 0.3
- Eigenvector: 0.8

Max:
- Degree: 0.5
- Eigenvector: 0.5

Wer wäre am besten als Gruppenleiter:in geeignet? Begründe deine Entscheidung anhand der Werte.

---

InstaHub-Community

Du analysierst die Follower-Beziehungen in einer InstaHub-Community von Hobby-Fotograf:innen.

1. Handelt es sich bei Follower-Beziehungen um einen gerichteten oder ungerichteten Graphen? Begründe deine Entscheidung.

2. Welches Maß eignet sich am besten, um herauszufinden...

   • wer die meisten Menschen direkt erreicht?
   • wessen Fotos von einflussreichen Accounts geliked werden?
   • wer gut vernetzt ist mit anderen einflussreichen Fotograf:innen?

---

Praktische Analyse

Hier sind die Freundschaften in einer Schulklasse mit 12 Schüler:innen:

Anna ist mit Ben und Clara befreundet. Ben ist mit David befreundet. Clara ist mit Emma befreundet. David ist mit Finn befreundet. Emma ist mit Finn befreundet. Greta ist mit Hans und Kim befreundet. Hans ist mit Ida befreundet. Ida ist mit Jan befreundet. Kim ist mit Leo befreundet. Leo ist mit Jan befreundet.

1. Handelt es sich um einen gerichteten oder ungerichteten Graphen? Begründe.
2. Erstelle einen Freundschaftsgraph (zeichne oder nutze das Colab)
3. Finde alle voneinander getrennten Freundschaftsgruppen
4. Schau dir die Klassensituation an:
   • Wie gut ist der Zusammenhalt in der Klasse?
   • Welche Probleme könnte es geben?
   • Was könnte man tun, um die Situation zu verbessern?

---

Social Media Manager:in

Du bist Community Manager:in bei InstaHub und sollst die Vernetzung in einer großen Fotografie-Community verbessern. Du überlegst, dafür eine Netzwerkanalyse zu nutzen.

1. Handelt es sich bei der Follower-Struktur um einen gerichteten oder ungerichteten Graphen? Begründe.

2. Überlege dir:

   • Was könntest du durch die Analyse lernen?
   • Welche Risiken gibt es für die Community-Mitglieder?
   • Wie könnten die Ergebnisse missbraucht werden?

3. Wie würdest du...

   • die Daten sammeln, ohne die Privatsphäre zu verletzen?
   • die Ergebnisse nutzen, um die Community zu verbessern?
   • mit sensiblen Erkenntnissen umgehen (z.B. wenn du "Cliquen" oder ausgeschlossene Mitglieder entdeckst)?

4. Schreibe drei wichtige Regeln auf, die du beim Umgang mit den Daten beachten würdest.